Business — Banking — Management — Marketing & Sales

The loss distribution results from the portfolio value distribution. The loss distribution is the mirror image of the portfolio value distribution. From the loss distribution, all loss statistics, including credit risk VaR and economic capital, derive. However, there are several alternative options for calculating them.

Portfolio Value and Loss Distribution

The loss calculations from the value distribution require a starting point to determine the downside variation that counts as a loss. All loss statistics result from the loss distribution and the starting point for calculating losses at the horizon. We discuss alternative choices in the next subsection. The notations used are:

Current date = 0 Horizon date = H

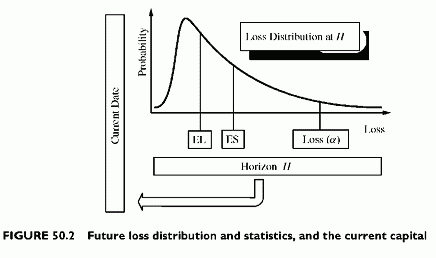
Portfolio loss percentile at the a confidence level = L_p(a)

Portfolio capital at the a confidence level = K_p(a)

Portfolio expected loss = EL_p

Portfolio contractual revenue = R_p

Revenues net of EL_p = expected spread (ES) = R_p — EL_p

The capital K_p depends on L_p(a), and on various options for dealing with EL_p and revenues Rp. Figure 50.2 visualizes the various calculations, once the horizon H is specified, for calculating the loss distribution.

Calculation of Losses

There is no obvious starting point for the calculation of losses. The loss is a difference between a reference portfolio value, used as origin, and other lower future values. The issue is to choose the reference value from which deviations are losses. The various starting points for calculating losses and capital are:

• The current value of the portfolio.

• The expected value at the horizon date.

• The expected value at the horizon conditional on no prior default.

For a default model and using book values only, the issue is much simpler to solve. The value under no default is the book value. Hence, losses start at aggregated book value as of current date. The accrual revenues serve for absorbing losses, as capital does. However,

only excess revenues over expected loss are available for such purposes. Therefore, capital should be net of the excess revenues over expected loss:

The loss percentile uses the current value V₀ as a zero point for losses.

For a full valuation model, the issue is more complex. The current value of the portfolio appears as a natural reference. However, it differs from the expected value at the horizon due to several factors: revenues between the current date and the horizon that increase the portfolio value at the horizon; migrations; roll-down effect. The expected value at the horizon embeds revenues, is directly comparable to horizon losses because of the time value of money, and appears as a better choice for counting losses. Unfortunately, it also embeds the expected loss instead of providing a clear-cut separation between expected loss and value.

For any facility, the expected value is the expected value under no prior default times the survival probability, plus the value given default, which is recovery, times the default probability (1 minus the survival probability). The equation is:

Since V_H jno default is random, it is necessary to use its expected value. The equation above assumes that V_H j_default is certain, which is only a simplification. The equation shows that the expected value embeds the expected loss. The expected value of the portfolio under no prior default does not. It results from the distribution of values at the horizon under matrix valuation, when eliminating transitions to the default state. It provides a solution for separating the expected loss from the expected value at the horizon. Capital follows the same equation as above:

The difference is that the loss percentile results from full valuation at the horizon rather than the initial book value and the expected value under no default is the starting point for counting losses from the value distributions.

KMV Portfolio Manager uses the expected value under no default for counting losses. Credit Metrics shows the current value, and does not calculate the expected value under no prior default. Both current value and expected value conditional on no prior default are feasible choices for calculating the loss distribution.

Expected Loss

For a default model, the expected loss is the expectation of all book value losses at the horizon. Under full valuation, the expected loss depends on the starting point, the current value or the expected value under no prior default. Using the current value as the zero loss point, the expected loss is:

Defining Capital

Once the loss distribution and the expected loss are determined, it remains to define the capital. Capital is the gap between a loss percentile L_p(a), if a is the level of confidence, and one of three possible starting points. These are the zero loss point, the expected loss, or the expected revenue. Since revenues might serve to offset some losses, there is a case for calculating capital in excess of expected revenue minus expected loss, which is the definition of the expected excess spread. Adding surviving facility revenues to the value at the horizon would reduce all loss values and shift to the right the loss distribution and its mean. The options are:

• Use capital in excess of the zero loss, when there is no provisioning of expected loss, so that capital absorbs both expected and unexpected losses.

• Use capital in excess of expected loss, if there is economic provisioning.

• Use capital in excess of expected revenue minus expected loss between now and the horizon, considering that revenues serve as a cushion contributing to absorb a fraction of the unexpected losses and that economic provisioning of losses is effective.

A common practice is to express capital as a multiple of loss volatility LV_p of the portfolio. This multiple derives from the prior determination of the loss distribution and the loss statistics serving as the zero point for capital. It is empirical rather than an ex ante multiple such as those of the normal distribution. Once all statistics are calculated, it becomes possible to write capital as a scaled factor of loss volatility:

This is a convenient formulation. The most important application of this formulation is capital allocation based on the risk contributions to the portfolio loss volatility. Such risk contributions, properly defined, sum exactly to the portfolio loss volatility (see Chapters 51 and 52). With the multiple m(a), it is easy to convert these risk contributions to the portfolio loss volatility into capital allocations. The loss percentiles result from the simulated distribution of portfolio values.

Discounting Future Losses to Present

Since loss values are at the horizon, they should be brought back to the current date to determine capital properly. A rationale for the choice of discount rate is as follows. Since capital is available today to meet future losses, we can invest it risk-free and get (1 + y_f) times the current capital at the horizon of 1 year. If the risk-free rate is 5% and we have 100 today as capital, we will have 105 in 1 year. Therefore, we need to match the proceeds from investment of capital with horizon losses. This is equivalent to matching the current capital with future losses discounted at the risk-free rate. Therefore, this discount rate is not the cost of capital of the bank, but the risk-free rate. This rule implies that capital should actually be invested in risk-free assets. If not, capital would generate higher revenues than the risk-free revenues, but it would also trigger additional risk, requiring additional capital, etc. The rule has a feedback effect on RaRoC calculations, because it requires adding to the revenues of any facility the revenues from the capital invested in the risk-free asset. Figure 50.3 shows loss statistics and economic capital.