Business — Banking — Management — Marketing & Sales

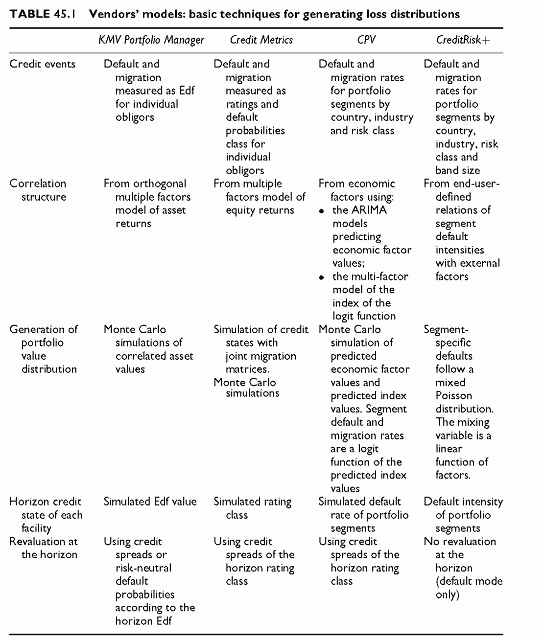
Table 45.1 provides an overview of the model specifics for generating portfolio value distributions at the horizon. The analytical distributions and the joint migration matrices are not as general as the Monte Carlo simulations. For Monte Carlo simulations, multi-factor models serve to generate correlated asset returns of correlated economic indexes, from which defaults and migrations result. The correlations result from the common dependence on several factors of the risk drivers. To generate correlated returns with a preset variance-covariance structure, the Cholevsky decomposition of the variance-covariance matrix is a popular technique. Factor models serve both to measure correlations and to generate correlated factor values by varying the factors on which risk drivers depend. In this case, the Cholevsky decomposition serves to generate correlated factor values converted into risk driver values, and finally into correlated default or migration events.

MODEL SPECIFICS

The following subsections provide a qualitative overview of the various model specifics. Details are given in the corresponding chapters.

KMV Portfolio Manager

KMV Portfolio Manager uses Monte Carlo simulations to generate correlated asset values of each firm. The model operates both within KMVs universe of listed firms and with

end-users preset default probabilities mapped to internal ratings. The end-user can use KMVs modelled expected default frequency (Edf ©) or specify directly the default probabilities through a table mapping internal ratings to Edf. To simulate the asset values at the horizon, KMV uses its multi-factor model of asset values with orthogonal factors. The variances and covariances result from the coefficients of orthogonal factors.

Revaluation at the horizon uses either credit spreads corresponding to the final credit state or the KMV specific risk-neutral Edf, allowing risk-neutral revaluation of the banks transactions at the horizon.

The result is a portfolio value distribution resulting from both migrations altering the value of facilities maturing after the horizon and default events between now and the horizon. The value at horizon statistics, mean, volatility and value percentiles, result from the numerical calculation of the portfolio value distribution. KMV Portfolio Manager also provides an analytical approximation of the loss distribution. Chapter 47 provides an example of such an analytical distribution.

Credit Metrics

Credit Metrics uses both joint migration matrices and Monte Carlo simulations to generate the final credit states of a facility. The joint transition matrix technique serves to determine all possible transitions for any pair of firms, depending on their initial states, between now and the horizon. With a large number of firms, these transitions result in a continuous distribution of the portfolio values. Each final state of an obligor is a rating class. Mapping rating classes with credit spreads allows revaluation according to the horizon credit state. The alternative solution is to use Monte Carlo simulations, as KMV does. The process is similar. The differences are the usage of the equity return correlation structure, and the mapping of final credit states to ratings for a valuation at the horizon based on credit spreads.

Econometric Models

The econometric modelling of the loss distribution (CPV) follows a simple framework. For each portfolio segment, there are default and migration rates. The default rates per segment depend on common economic factors through a logit function. The logit function uses as input an index that is a linear function of economic variables, or factors, and fits the time series of default rates of portfolio segments. By generating random values of economic factors, it becomes possible to generate correlated random values of these default rates. The migration rates change accordingly, so that the sum of all migration rates within a risk class, inclusive of the migration to the default state (with a frequency equal to the modelled default rate), is 1.

The technicalities of the econometric approach result from the multiple models involved in the process. The default rates of portfolio segments are a logit function of an economic index, which is a linear combination of economic factors plus an error term. Looking forward, all economic factors have uncertain values. Therefore, it is necessary to generate the distributions of each of the predicted values of these factors. CPV uses the Auto Regressive Integrated Moving Average (ARIMA) time series model to obtain future predicted values of factors. Future values become conditional on known past values of factors and of error terms of the ARIMA fit. The distribution of the future values of a single economic factor around its predicted value is that of the error term. With only one factor, it is easy to generate such a distribution since we know the standard error of the residual from the fit. With several factors, the problem gets more complex because all factors correlate as well as the error term of each ARIMA model fitting the predicted value of each factor to its past values and errors. Therefore, it becomes necessary to impose the correlation structure on all factors and all ARIMA residuals. CPV uses the Cholevsky decomposition to perform this task. In the end, we obtain correlated values of the indexes that drive the default rates of segments, and correlated values of these default rates through the logit function relating them to the common factors.

The model captures economic trends and cyclical movements, and uses relations between observable variables, making interpretation easy. This feature is an important strength of CPV, since the simulations embed the effects of the economic cycles over future horizons. The model allows us to test explicitly a discrete number of economic scenarios, instead of using the full simulation model, to see how they influence the portfolio. In such a case, instead of drawing a large number of random values of indexes driving default rates, we simply select a discrete scenario made of selected values of economic variables. The process provides a final rating class for each scenario and for each portfolio segment. Revaluation of facilities within the portfolio segments uses the credit spreads corresponding to the simulated values of the default rate. The ultimate result is a portfolio value distribution at the horizon.

The drawback of the technique is that it is data intensive. Also, CPV is an open framework, which is a desirable property since it allows flexibility in model design and variable selection. On the other hand, it is not a self-contained model such as KMV Portfolio Manager, which provides the outputs using its own proprietary model rather than requiring modelling by end-users.

Analytical Distributions and CreditRisk+

The CreditRisk+ approach is an elegant methodology because it is entirely analytical. It relies on the mixed Poisson distribution, whose parameter is the density of defaults per unit of time, a parameter similar to a yearly default probability. This distribution models an independent number of defaults only. This does not capture size discrepancies between exposures, or correlations. To remedy the first limitation, CreditRisk+ requires using portfolio segments by exposure size (in practice, exposure is within predefined bands), risk class and recovery class. This is necessary to convert the number of defaults into losses under defaults given discrepancies in both exposures and loss under default sizes.

Within each segment, the mixed Poisson distribution applies if defaults are independent. Without correlation, it is a simple task to combine the Poisson distributions of the different segments. The sum of Poisson variables is also a Poisson variable whose Poisson default density sums up all Poisson parameters.

The time intensity parameter makes defaults dependent on time, which is a useful feature for modelling the time to default. When aggregating distributions over all segments, we obtain the distribution of the portfolio loss time profile. This can help to schedule provisions or identify worst-case time profiles of losses.

In order to capture correlations, CreditRisk+ uses a property of mixed Poisson distributions. The principle is as follows. A mixed Poisson distribution depends on a default intensity that is the product of a mixing variable and an average default intensity. The mixing variable allows the default intensity to vary depending on whatever factors influence it. A property of mixed Poisson distributions is that a sum of such distributions is also a mixed Poisson distribution, even when the mixed variable depends linearly on external factors. This allows CreditRisk+ to make the mixing variable dependent on user-defined factors. The dependence on a common set of factors makes the mixing variables of all segments correlated. At this stage, it is possible to numerically calculate the loss distribution using the long-term average default intensity per segment plus the user-defined dependency on common factors. To obtain an analytical loss distribution, CreditRisk+ uses another property. When the mixing variable follows a gamma distribution, the resulting loss distribution is a negative binomial distribution.

CreditRisk+ has many appealing properties. Since the loss distribution is analytical, it is simple and fast to calculate. The time intensity parameter makes defaults dependent on time, which is a useful feature for modelling the timing of losses. It is also a simple task to consider various scenarios by changing the values of the mixing variables. On the other hand, CreditRisk+ does not model the relative magnitude of general and specific risk, which is user-defined, and is a default model only. It also imposes restrictions with respect to the definition of portfolio segments and relies on several attractive properties of mixed Poisson distributions, but necessitates restrictive assumptions to implement them.

Portfolio Loss Distributions: Example

This chapter details simple examples of loss distributions. Its purpose is twofold:

• To show how correlations alter the loss distribution of portfolios using a very simple portfolio made of two obligors. The credit standings of obligors correlate, which influences the loss distribution. The measures of risk are the Expected Loss (EL), the Loss Volatility (LV) and the Value at Risk (VaR), which results from the loss percentile values L(a) at various preset confidence levels a.

• To provide the full calculation of joint default probabilities and the relations between the default correlation, unconditional and conditional default probabilities of each obligor.

To detail fully the effect of correlations, starting from independent defaults helps. In this case, under default mode only, there are four cases: no default, a single default of the first obligor, a single default of the second obligor, or joint default. This makes it very easy to track any change in loss distribution resulting from correlation. Moreover, the detailed calculation of conditional and unconditional probabilities shows how the probabilities of single or joint defaults within a portfolio relate to the standard (unconditional) default probabilities of obligors and to correlation.

The first section details the loss distribution with a two-obligor portfolio having independent individual risks. The second section constructs a two-obligor loss distribution given default correlation. The next chapters (47 and 49) detail further the correlation effect using the techniques of the main portfolio models.