MODELLING CORRELATIONS FROM CREDIT RISK FACTORS
Category: Risk Management in Banking
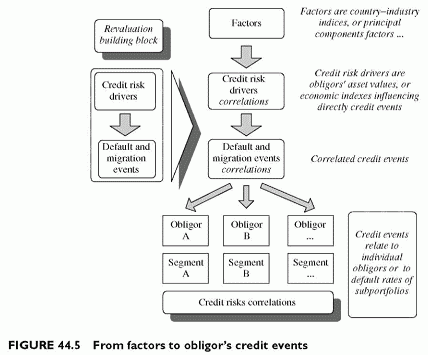
Figure 44.5 provides an overview of the modelling of correlations between individual risks, from common risk drivers and factors. Chapter 31 explains the essentials of factor models. The revaluation block models the relationship between credit risk drivers and credit events, but it does not generate any correlation as such. The purpose of the revaluation building block of models is to link drivers to risks. The revaluation block does not capture correlations. These derive from the correlations of the risk drivers. The next subsections detail the specifics of models related to the correlation building block.
Credit Risk Model Specifics
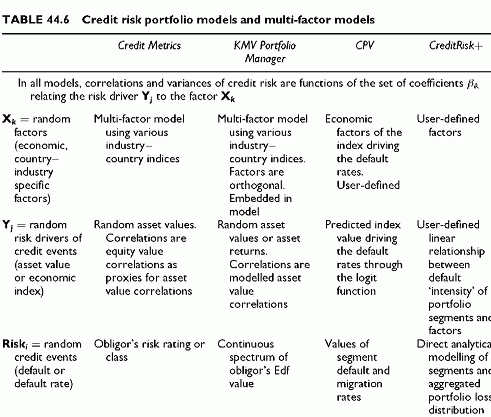
The different models use different factors to correlate credit drivers and, ultimately, credit events. In the credit risk universe, the random variable Y,- explained by factors is a credit risk driver of obligor i. Credit risk drivers are unobservable asset values in the option theoretic approach, or predicted values of an economic index in the CPV framework.
Multi-factor models relate these credit risk drivers to a number of factors. Some are explicit, such as the observable economic variables of CPV, while asset values are not, but they are all functions of real variables. KMV Portfolio Manager uses orthogonal (independent) factors to model asset returns of obligors. Each factor represents multiple dimensions difficult to disentangle. On the other hand, independent factors make it much easier to model credit risk correlations within a portfolio, as the derivation of correlations
from the coefficients illustrates in Chapter 31. CPV uses economic indexes to correlate default rates of portfolio segments.
KMV Portfolio Manager
KMV measures correlations between modelled asset values derived from equity and debt values of obligors. The correlations between modelled asset values result from a multi-factor model, using orthogonal factors such as regions, or industry indices, obtained using principal component analysis. Orthogonal factors facilitate the calculation of asset value correlations from the coefficients of the multi-factor model. Asset values are the direct risk drivers, serving to correlate the Edf of different obligors through the option theoretic framework.
Monte Carlo simulation uses random independent asset returns to find, for each run, the risk-adjusted value distribution of a facility. The revaluation block uses either credit spreads and matrix valuation or risk-neutral modelled Edfs. KMV aggregates over the entire portfolio the facility value distributions to obtain that of the portfolio. The R2 provides a direct estimate of the general versus specific risk. When no fit is available, for private firms for example, it is necessary to specify the R2, the ratio of general to total risk, using for instance the average over all firms. See Chapter 48 for additional details.
Credit Metrics
Credit Metrics uses observable equity return correlations as proxies of unobservable asset value correlations. To model such correlations, it relies on a multi-factor model. The
model derives pair correlations from coefficients of the factor model. The joint migration matrices result from equity return correlations. They serve to simulate the credit standing of pairs of obligors at the horizon, and provide the rating distributions at the horizon for all obligors, from which risk-adjusted facility values derive. Alternatively, Monte Carlo simulations generate correlated asset value returns, using the equity correlation structure.
This procedure does not adjust asset values and correlations for the obligors leverage that influences both equity values and correlations. By contrast, KMVs usage of asset values and correlations undoes the leverage effect when it relies on unlevered and unobservable asset values.
Credit Portfolio View
CPV models default rates of subportfolios logit functions of an economic index Y.This economic index is a linear function of economic factors, analogous to a multi-factor model. An intermediate building block serves for using predicted values of economic factors, to use predicted values of default rates rather than current ones. The correlations of predicted values result from the multi-factor model. The predicted values of common economic factors derive from Auto Regressive Integrated Moving Average (ARIMA) time series models and depend on their lagged historical values and error terms.
The intermediate risk drivers of the particular portfolio segment i default and migration rates are the future random value of one economic index influencing the credit risk of obligors within this segment, or CR= ,t+1. The subscript t + 1 represents the horizon date and t the current date. This index is a linear function of predicted values of economic factors Xk;t+1. Finally, each predicted value of each factor depends on Xk, their lagged values and the residuals. The default rates are a logit function of the predicted index Y,;t+1, which depends on the Xk;t+1 through a linear multi-factor model. The economic factors and residuals of the , t+1(X1; t+1, X2, tXk, t+1, e{, t+1) function are not independent and comply with a variance-covariance structure.
The technique for generating correlations is analogous to those of KMV and Credit Metrics. However, the model differs from these through three major features:
• It measures aggregated default rates, not individual default events. These are observable, unlike individual default events of surviving firms that need modelling.
• It uses economic factors to capture the cyclical dynamics rather than modelling correlated unobservable events. Neither KMV not Credit Metrics link explicitly the credit risk to cyclical dynamics.
• It does not rely on the option framework to derive default rates, but uses a logit function of an economic index linked to economic factors.
CPV provides a framework for model fitting, but leaves it to end-users to choose whatever fit they need depending on available data and portfolio segment definitions. CPV uses Monte Carlo simulations to generate default rate and migration rate distributions for portfolio segments, thereby assigning distributions of correlated final ratings to all facilities. It revalues facilities using the simulated default rates for the entire portfolio to get a portfolio value for each run, and as many as there are runs of simulations. See Chapter 48 for additional details.
CreditRisk+
CreditRisk+ takes another path. Like CPV, it models default rates of subportfolios. Unlike CPV, it requires using size bands as a criterion, in addition to risk class, to create subportfolios. CreditRisk+ models directly loss distributions of subportfolios as mixed Poisson distributions, whose mixed Poisson parameter is q x d, q being the random mixing variable and d being the default intensity analogous to a default probability. The mixing variable allows us to change the default intensity through time for instance.
The default intensity for segment i depends on the mixing variable q,-, which allows the default intensity to vary, where i is the segment index. This distribution has a Poisson parameter, which is the product of the random variable q,-whose expectation is 1, with the usual Poisson parameter. The basic model ignores correlations. The correlation is an add-on to the basic structure.
In order to model correlations, CreditRisk+ makes the mixing variable q,- sensitive to a common set of external factors. The sensitivities to these factors vary across portfolio segments:
q,- = #1 x Xi + A-2 x X2 + A3 x X3 + • • •
This effectively correlates the mixing variable q, of segments, resulting in correlated loss distributions per segment. Then, it aggregates the loss distributions of all segments. Since such a linear relationship is deterministic, all credit risk is general and there is no specific risk per segment, which is a risk independent of all factors. CreditRisk+ suggests adding another independent segment for specific risk.
The sensitivities and factors are user-defined, and there is no framework for modelling these factors. CreditRisk+ does provide some guidelines for fitting such factors and default probabilities to observed data. Notably, it suggests linking the random q, variables to actual observed default volatility as observed from time series. The external parameters as well as the sensitivities to these external factors are end-user-defined. Hence, CreditRisk+ provides a methodology to embed correlations through sensitivities to external factors, but does not specify how to model the sensitivities. The modelled distribution of losses remains entirely analytical (see Chapter 47).
Overview of Portfolio Model Correlation Building Blocks
KMV Portfolio Manager and Credit Metrics are fully self-contained models. CPV provides a modelling framework but lets end-users adjust the fits to selected parameters of their choice. CreditRisk+ remains open for correlation modelling. On the other hand, it provides the easiest calculations, because it uses an analytical loss distribution rather than Monte Carlo simulations. See Table 44.6.
General and Specific Risks in Multi-factor Models and Correlation Effects
Normally, the factors influence results from statistical fits. Statistical fits also provide the characteristics of the error terms. This is the case for all firms included in KMV Credit Monitors universe.
Frequently, the universe of bank portfolios does not include such firms, and there is no modelling available of factor influences. This requires providing an estimate of the fraction of specific variance resulting from the error term (or, alternatively, of the variance from all common factors, which is general risk). In such a case, the specific risk becomes a control parameter of the model. The higher the specific risk, the lower the correlation effect and, conversely, increasing the systematic risk generates a higher correlation. The final loss distribution is very sensitive to the correlation effect, so that the control values used for general risk are important.
Hence, the ratio of specific to total risk becomes an input for private firms whenever there is no model allowing us to capture directly the general risk. KMV Portfolio Manager provides the ratio of general to total risk for end-users and also allows end-users to assign a value to this parameters. The ratio of general risk to total risk is the R2 of the multi-factor regression model. Stressing this R2 is equivalent to increasing the general risk and, therefore, the correlations. This increases the portfolio risk. Credit Metrics allows for a similar stress testing of correlations. Similarly, CreditRisk+ does not specify any fit to common factors, making it necessary for the end-user to specify a value for specific risk. The correlations are highly sensitive to this term, and so is the loss distribution of the portfolio.
Generating Loss Distributions: Overview
Factor models serve both for modelling correlations between risk drivers and generating correlated credit risk events with simulations to construct the loss distributions of portfolios. This chapter addresses the second issue, assuming that the variance-covariance structure of risk drivers is available from factor models. The generation of correlated loss distributions is critical since all portfolio loss statistics derive from these distributions.
Most vendors models generate correlated loss distributions with Monte Carlo simulations. The chapter reviews the specifics of different models. KMV Portfolio Manager uses Monte Carlo simulations of modelled asset values of obligors. Credit Metrics uses both Monte Carlo simulations and the joint migration matrix technique. Credit Portfolio View (CPV) uses Monte Carlo simulation of economic factors. CreditRisk+ is a notable exception with its analytical loss distribution. Subsequent chapters further detail the techniques and provide examples of simple implementations. This chapter summarizes all subsequent chapters (46 to 49) detailing the loss distribution modelling techniques.
The principle of simulations is to generate correlated random credit risk drivers complying with a given variance-covariance structure. The risk drivers are asset values for KMV Portfolio Manager and Credit Metrics, although correlations have different bases (asset values versus equity prices). They are the economic variables driving the default rates in CPV.
In many instances, assigned default probabilities summarize all inputs for deriving loss distributions, except correlations between credit risk events. Two techniques serve as a simple correlated default simulator bypassing the unobservable asset values. The simplest solution correlates standardized normal distances to default to obtain correlated defaults. The distance to default measures the risk and varies inversely with default probability. Alternatively, correlating the stochastic processes driving the asset values of each obligor also generates correlated defaults. In this case, asset values follow lognormal distributions. The same general principle applies under the economic framework of CPV. Random values of economic indexes are converted into default rates through the logit function. Each simulation run comprises four steps:
• Generating a set of correlated values of risk drivers, asset values or economic index values.
• Converting each set of driver values into credit events, default or migration, using the option model (KMV and Credit Metrics) or the logit function (CPV).
• Aggregating the facility values to provide the portfolio value.
• Repeating the process for each new draw of sets of values of credit risk drivers. There are as many portfolio values at the end of the process as there are simulation runs. Together, they make up the portfolio value distribution.
There are analytical proxies of portfolio loss distributions. The most accomplished is that of CreditRisk+. These techniques provide very convenient numerical formulas to determine loss statistics and loss percentiles, bypassing the calculation intensive simulation process. The drawback is that such proxies significantly deviate from simulated distributions, presumed better approximations of unobserved actual distributions.
The first section provides an overview of the loss distribution module. The second section summarizes the specifics of each of the main models.