Business — Banking — Management — Marketing & Sales

Enhancing the risk-return profile of the portfolio can minimize risk given return, increase return at constant risk, or improve both if the portfolio structure is inefficient. In addition, when removing funding constraints, it is no longer necessary to trade-off risks and return within the portfolio by changing the exposures. It becomes necessary to decide along which direction portfolio expansion is more efficient. We illustrate through simple examples the trade-off under constraint of risk and return and the case of portfolio expansion.

Trade-off Risks within Limits

We can use the above sensitivity analysis to illustrate what happens when we increase the exposure in different segments. For this purpose, we use a portfolio segmentation into high-risk and low-risk obligors, because it is straightforward.

When we increase exposure on high-risk obligors by 20%, the loss volatility increases by 6.56%. If we increase the exposure by 20% on low-risk obligors, the loss volatility increases by 15.12%. This is more than twice as much. The ratio is 15.12/6.56 = 2.305. This means that we can trade-off exposures between high-risk and low-risk exposures with a ratio of 2.305 to 1 at constant risk, the risk metric being loss volatility. An additional exposure of 1 on the low-risk obligor is, on average, equivalent to 2.305 of additional exposure on low-risk obligors. This assumes that we hold constant the structure of the exposure and the loss given default. In practice, more accurate calculations are necessary, to revaluate the portfolio loss volatility.

Portfolio Optimization

Portfolio optimization under a global funding constraint means:

• Reducing risk, at a constant return.

• Increasing revenue, at the same risk.

If we assume the spread as a percentage constant, the issue is to define the portfolio weights leading to a more efficient risk-return profile. Formally, this is the well-known problem of maximizing return given risk, or minimizing risk given return, a constrained optimization problem. In practice, enhancing the risk-return profile through trade-off of exposures requires only simple calculations as a first approximation.

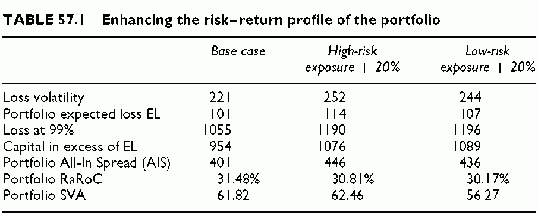
From Table 57.1, we see that the capital and Shareholders Value Added (SVA) expand when expanding the exposures. However, expanding the low-risk exposures decreases the RaRoC and the SVA. Therefore, it is better to expand the high-risk exposure, which slightly improves the SVA, even though it deteriorates the overall RaRoC. In this example, the base case is the best of the three cases (Figure 57.3).

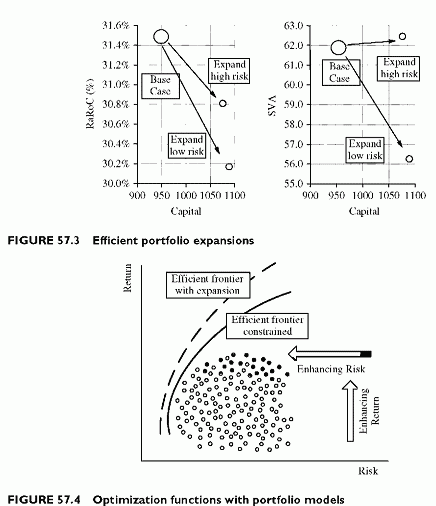
Portfolio optimization follows these lines. Restructuring exposures generates new risk-return combinations. Some dominate others. These make up the efficient frontier. Then, it becomes technically a simple matter to see how to move to various points on the efficient frontier by changing the portfolio structure. This requires a full optimization module in the portfolio model, because both capital allocation and return are allowed to vary (Figure 57.4).

Optimization under funding constraints differs from optimizing the portfolio expansion. In addition, a full optimization model should recognize the limits imposed on business volume, by risk class, industry and country. Economically, limits are sub-optimal. On the other hand, portfolio expansion remains business-driven, and the optimization should well integrate both the economic efficiency and the business policy. The optimization module helps, but is not a substitute for business policy and limits.

KMV Portfolio Manager and Credit Metrics illustrate the two philosophies. The first model embeds a constrained optimization module providing various optimized outputs, such as:

• Optimization at constant risk.

• Optimization at constant return.

• In addition, it visualizes the efficient frontier given the funding constraint.

Modelling the efficient frontier under no expansion guides the rebalancing of the portfolio through exposure sizes. Revising limits, adjusting the final take (the commitment size retained by the leading bank) and securitizations are examples of business transactions that rebalance the portfolio.

Credit Metrics does not offer optimization functions. However, it provides the marginal risk contribution, rather than the absolute risk contribution. This is theoretically more adequate when considering expansion of exposures along various segments or individual obligors.

Both models allow recalculation of the marginal contributions anyway. With small exposures, these do not differ significantly from the absolute risk contributions. With large exposures, the portfolio model has to run with and without new exposures, repeatedly if necessary.

Models provide valuable insights for restructuring and expanding, or contracting, some portfolio segments or individual exposures. In fact, without such models there is no way to compare various what if scenarios and rank them in terms of their risk-return profiles.

Credit Derivatives: Definitions

Credit derivatives (CD) are a major innovation in that they offer credit risk protections that were not available until recently. The potential for managing and hedging portfolio credit risk seems considerable. Until the appearance of credit derivatives, and besides insurances, there was no way to hedge credit risk, once originated, other than by restructuring a transaction, which is an uneasy process.

Credit derivatives provide this possibility without altering the actual assets held by a bank. In addition, they benefit from the potential depth of the market, driven by the attractiveness that they provide to sellers, or investors, in these instruments. Because of their innovative characteristics, they offer plenty of new opportunities for major players, such as banks having exposure to credit risk, and for investors willing to sell protection in exchange for a credit exposure and the corresponding return.

Credit derivatives perform classical functions embedded in standard products providing insurance on credit risk. They are like back-to-back deals, where a third party allows its credit standing to be used as a guarantee to make a market between counterparties who, otherwise, would not enter into a transaction directly. Credit derivatives perform similar functions with more flexibility and are not simple substitutes for traditional guarantees. They provide protections for underlying assets that often differ from those effectively held by protection buyers, and they allow both buyers and sellers of protection to customize their credit risk exposures. Credit derivatives are attractive because they provide flexible hedges to the protection seekers and new investment opportunities to the protection sellers. In order to organize and develop the market, the terms of these contracts have evolved sufficiently to make transactions feasible.

There are three basic types of credit derivatives:

• Credit default products providing a specified payment under default events.

• Total return swaps exchanging revenues and capital gains-losses of the underlying assets.

• Credit spread products allowing positions to be taken on future spreads.

The spectrum also extends from credit derivatives to other products providing further flexibility, such as basket swaps, credit-linked notes or sovereign risk derivatives.

This chapter is a broad overview of credit derivatives. The first section introduces their specific functions and describes who are the key players. The second section details the main definitions and key terms for understanding the characteristics and mechanisms of these products. Subsequent sections describe the different types of credit derivative products and the rationales of using them as protection buyers or protection sellers.