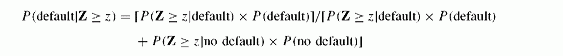Business — Banking — Management — Marketing & Sales

Scoring provides information on the credit standing of a firm. Therefore, the probability of default given the score S differs from the probability of default under no information on S. If we use scoring to discriminate between firms that are likely to default in the future and firms that are not, we can infer from the score the conditional default probabilities given the score value. Without knowledge of the score, we would assign the same default probabilities to all firms. This is the prior probability of default. With scoring, we can differentiate them according to the score values using Bayes theorem.

Since scores convey information about risk, the probability of default given the score differs from the same probability estimated without having the score value. The posterior probabilities transform the scoring model into a default model. If we pick up a firm, we calculate its score value Z = z. The issue is to find the default probability conditional on ascore Z greater than the value z obtained for a particular firm. We assume that higher scores correlate with default risk.

Bayes theorem allows us to move from unconditional, or prior probabilities, to conditional or posterior probabilities, once we add some information relevant to the occurrence of Z. The formula for Bayes theorem relates unconditional and conditional probabilities of two events, one, D, being a default event, and the other being anything that provides information on the default event, such as a score Z from a scoring model of defaults. Bayes theorem states that:

The Zeta Score

A famous score is Altmans zeta score (Altman et al., 1977; first contribution 1968). This is a multivariate model built on the values of selected ratios and categorical measures. The Z-score model applies to a large variety of borrowers, from small to medium size firms. The basic Z-score model is public. It uses five variables to discriminate between obligors. These are:

• Working capital/total assets.

• Retained earnings/total assets.

• Earnings Before Interest and Tax (EBIT)/total assets.

• Market value of equity/book value of liabilities.

• Sales/total assets.

The discriminant function is linear. All ratios have a statistical coefficient in the function:

Accordingtothe valueof Z, the firm is closer or not to the defaulting firms group characteristics than to the survivor group. The value of Z measures the likelihood of default. High scores indicate low likelihoods of failure, and conversely. The implementation implies that we should define a range of values of Z in order to make a decision. A typical utilization of such a model requires defining boundary values for Z such that:

• Below a lower bound, the firms likelihood of failure is high.

• Above an upper bound, the firms likelihood of failure is low.

• Between the upper and lower bounds, we do not know, because the model does not discriminate well the two categories.

These cut-off values of scores serve to classify obligors into good or bad categories, or in between.

Recent versions of the zeta-score model extend the coverage to larger firms than before. Variables are return on assets, stability of earnings, debt coverage ratio, retained earnings, liquidity as measured by the current ratio, capitalization and the logarithm of the size of assets.

The benefit of scoring is to speed up the credit decisions and the rating process. The drawbacks are:

• Some critical characteristics, other than ratios, might be relevant and not included in the discriminant function. For example, management quality for small firms is critical.

• There are no conceptual foundations to scoring, except that the effects of variables are in line with intuition. This is not a drawback as long as the issue is the end result, not the conceptual foundations of the fitting process.