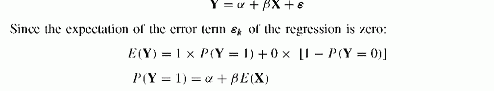Business — Banking — Management — Marketing & Sales

There are models dedicated to predicting binary events, such as defaults or non-defaults, or to scaling the probabilities that such events occur. Originally, they were behavioural models, used to predict two or more qualitative choices or behavioural responses, such as voting yes or no, ranking different products by consumer preferences, and so on. These models include the linear probability models and the more adequate logit and probit models. In what follows, individual means individual observation, an observation relating to any type of borrower, consumer or corporate:

• Binary models assume that individuals belong to either one of two categories only, such as defaulting firms and non-defaulting firms, depending on their characteristics.

• Multinomial models accommodate several categories, such as ratings, depending on their characteristics.

In addition, these models apply to:

• Classification in categories: categories (defaulters and non-defaulters) are nominal variables, such as yes and no. The goal is to achieve the highest number of correct classifications.

• Ordinal variables, which measure ranks, such as ratings, or numerical (cardinal) variables, such as default frequencies. The goal is to minimize the errors between values predicted by the model and actual values.

Ordered probit or logit models perform better with ranks (ratings) than other models considering each rating as a separate category, without any rank (ordinal) relation with other ratings. The principle of these models is to determine the probability that an individual with a given set of attributes will make one choice rather than an alternative choice. These models use an adapted multivariate regression technique. The explanatory variables are the attributes X,-.

Use of Logit and Probit Models

In practice, the logit and probit models are adapted for modelling:

• Default frequencies, which have values in the 0 to 1 range.

• Ratings, which are ordinal variables.

Simple regressions have strong limitations when modelling default frequencies, because these are necessarily within the 0 to 1 range. When fitting a linear regression between ratings and financial attributes, size, operating profitability, leverage, and so on, chances are that the model will provide outputs for some combinations of values that lie beyond the 0 and 1 bounds. In such instances, it is necessary to embed the constraints on predicted values from the very beginning. This is where logit and probit, applied to numerical variables, shine. Unlike regression models, which assume that the relation between rating and size, for example, is linear, these models do not suffer from the non-linearities observed between observable attributes.

The Basic Linear Model Drawbacks

The simple linear probability model explains the principles. The linear probability model is the simplest version of models of binary events. It makes the probability P of the event a linear function of one attribute X. In fact, we try to explain a binary variable Y,0or 1, with the attribute:

The model provides the value of the probability that Y equals 1. However, it does not comply with the constraint that all values of Y should be within the 0 to 1 range. This implies truncation to avoid such outliers. The probit-logit models avoid this drawback.

Probit and Logit Models

The probit and logit models address the problem of translating the values of an attribute X, whatever they are, to a probability that ranges between 0 and 1. In addition, an increase of X should correspond to an increase in probability, which is the dependent variable.

This allows an easy interpretation of the model. The argument of the logarithm P(Y)/[1 — P(Y)] is the odds of belonging to one group, or the ratio of the probability of belonging to that group to the probability of not belonging to that group. The logarithm of the odds ratio is the logit. When Y = 0, the logarithm is 1 and the odds ratio is 1, meaning that there are as many chances of belonging to one group as there are of belonging to the other, implying a common value P(Y = 0) = 0.5. One attractive feature of the logit model is that it transforms the issue of predicting probabilities into a linear model predicting the logarithm of the odds of a particular event. Once the model is fitted to data, we have the coefficients. The value Y = a + //X calculated for particular information is simply the logarithm of the odds ratio, and the exponential is the odds ratio itself.

The logit model has some drawbacks. When P(Y) = 0 or 1, the logarithm is undefined, making the regression inadequate. The remedy is to use grouped observations where we can observe the fraction of observations belonging to one group. This ensures that values will not reach extremes. Note that this applies for credit risk whenever we model the default rate within predefined segments. This applies to CPV. It also applies better to retail banking because segments defined by product type and borrower type are a typical way to model risk. Another drawback is that the variance of the predicted variable varies from one group to the other².

The Probit Model

The probit model performs similar functions to the logit model, but uses the normal distribution instead of the logistic distribution. Because the normal distribution is more complex than the logistic distribution, the model looks more complex. However, there are no practical differences with available statistical softwares. The probit model considers

Y as normally distributed and uses the cumulative distribution of the normal distribution.

Y can take any value, negative or positive. Once we have the X value, we have the Y value, and once we have the Y value, we have P (Y) through the equation making Y the normal inverse function of P(Y). There is a one-to-one correspondence between Y,which is unconstrained, and the probability P(Y):