VALUATION OF CREDIT RISK GUARANTEES, INSURANCE OR CREDIT DERIVATIVES
Category: Risk Management in Banking
The valuation of insurance, guarantee or credit derivative depends on the correlation between the credit risk of the two parties, the risk seller/buyer of a protection and the risk buyer/seller of a protection. Whether the protection is a third-party guarantee, an insurance or results from a credit derivative does not matter in terms of valuation. The main issue is what becomes of the joint default probability of the buyer of the protection and the seller of the protection. In general, it decreases far below the default probability of the borrower, which is the key to valuing third-party protection. The regulators do not provide full recognition of this double default effect and consider that the exposure transfers to the guarantor, which is inexact, even though it is more practical than a joint default probability calculation. This section focuses on the technical ways of valuing the joint default probabilities and on correlations that influence this probability. It does not address the legal risk issue, whose assessment is essentially qualitative. The first appendix to this chapter provides details of the calculations of joint default probabilities, and only the essentials are given in the main text.
The Valuation of Joint Defaults
The buyer of a protection, such as an insurance against the default of a direct borrower, hopes that the insurer (the guarantor) will not default if the direct borrower does. If the insurers probability of default does not depend on the borrowers default, the probability of both defaults is the product of the unconditional default probabilities and is very small. If the default of the borrower and the default of the guarantor correlate, the insurance gets weaker because the likelihood of the insurers default when the borrower defaults increases. Under positive correlation, the conditional probability of default of the insurer is higher when the borrower defaults than when he does not. A simple way to express default correlation is to assign a value to the conditional probability of default of the insurer given the default probability of the borrower.
To value guarantees, support, insurance and protection through credit derivatives, it is possible to recalculate the joint default probability of the pair of obligors, borrower and provider of protection, given correlation effects. The value of the protection is the difference between the standalone default probability of the borrower and the joint default probability, which is lower (unless support is negative), as shown below. The latter depends on the correlation between the risks of borrower and guarantor. This section uses this principle to value a guarantee. It ignores legal risk and the strength of the support relationship, because their assessment depends on legal issues and judgmental assessment. This allows us to address the valuation issue under a zero enforcement risk, but an assessment of this risk is necessary independently from any valuation of recoveries.
For rating purposes, it is possible to qualify and rate the borrower-third party relationship, based on the joint default probability since the specifics of the relationship are known by credit officers. A comprehensive rating system should include this component since the effects on risk might be very significant in many instances.
Joint Default Probabilities, Conditional Probabilities and Default Correlation
From an economic standpoint, any positive correlation between guarantor and direct borrower weakens the value of the guarantee, as intuition suggests. However, even a low credit standing guarantor can provide an efficient guarantee as long as his chances of defaulting when the borrower does are low. This is because joint default probabilities are, in general, much lower than standalone default probabilities. The Joint Default Probability (JDP) is:
JDP(both default) = P(borrower defaults and guarantor defaults)
It depends on the correlation between the default of the primary borrower and that of the guarantor. Usually, the correlation between the default events is positive because of underlying factors influencing credit standing, such as belonging to the same country-industry segment. If default events are independent, the joint default probability is the product of the standalone default probabilities. If there is a positive correlation, the joint default probability is higher than this product. Such principles are not equivalent, in general, to what intuition would qualify as a risk transfer. This intuition suggests that the lender is at risk with the indirect exposure on the insurer rather than on the primary borrower. This is not correct in general, but might be a proxy in some cases.
This section details joint default probabilities and conditional default probabilities. We use the following notation: B is the primary borrower, G is the guarantor or seller of protection (default derivative), b = P(B defaults) and g = P(G defaults) are the two default probabilities of B and G, P(B, G) = joint default probability of B and G = JDP(B, G),P(G|B) = conditional probability of default of G if B defaults, p = correlation between default events of two entities.
Using our notation rules, bold characters are random variables and italic characters their values. Default events are Bernoulli random variables d, whose values are either 1 for default or 0 for no default. Accordingly, dB and dG represent the random default events of B and G. There are straightforward relationships between conditional default probabilities and correlations. The second appendix to this chapter shows that joint default probabilities are easy to derive for a pair of obligors. The formula providing the default probability of a primary borrower B benefiting from a fully enforceable guarantee from the guarantor G is:
The Joint Default Probability of the Borrower and the Guarantor
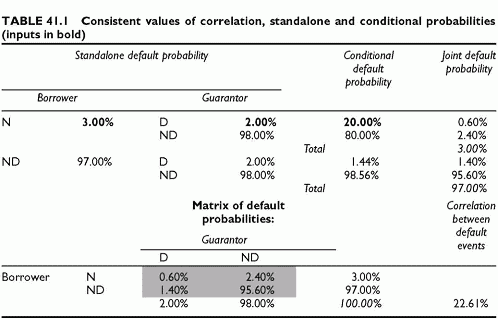
The numerical example below uses the general format for calculating numerically conditional probabilities based on unconditional probabilities and the correlation between credit events. The example starts from unconditional default probabilities. Defining at least one conditional default probability, plus the standalone default probabilities, is sufficient to obtain the full set of conditional probabilities and the joint default probability, as shown in the second appendix. In the example, we start from the conditional probability that G defaults given B defaults, here 20%. The entire set of joint probabilities follows, including the correlation between default events. The example is in Table 41.1. In the table, the inputs are in bold:
The final result is that the default correlation is 22.61% and the joint default probability of B and G is P(B, G) = 0.60%, much lower than the higher standalone default probabilities of B and G, respectively 3% and 2%. The value of the guarantee is the gain in default probability of lending to B alone versus lending to B with a guarantee from G. This gain is 3% — 0.60% = 2.40%. In terms of rating the credit to B, this is a very high increase in rating.
The Value of Third-party Guarantees and Correlations
When the correlation is 0, the default events are independent, the joint probability P(B, G) collapses to P(B) x P(G) and the conditional default probabilities become identical to the standalone default probabilities. The default of either one obligor has no influence on the default probability of the other. Under independence, the joint default probability is 2% x 3% = 0.06%. The default risk becomes 10 times lower than in the case where P(G|B) = 20%. The gain in default probability of B, compared to the case with no guarantee, is 2% — 0.06% = 1.94%. The guarantee turns a speculative grade rating into an equivalent Aa rating. This result holds even though the guarantor has a 3% default probability, equivalent to a speculative grade rating. An important conclusion is that a poor rating guarantor actually enhances significantly the default probability of the borrower.
When the correlation becomes positive, the joint default probability increases with the correlation. Figure 41.2 shows the relationship between the joint default probability of the primary borrower and the guarantor. The correlation increases the joint default probability, thereby decreasing the value of the guarantee. This relationship is linear, according to the above formulas. The unconditional default probabilities of B and G are respectively 3% and 2%. There are consistency constraints between unconditional probabilities, conditional probabilities and the correlation coefficient values. Therefore, it is not possible to pick these values independently. These constraints are explicit in the second appendix.
Implications
In order to convert the joint default probability into a rating, it is possible to use the rating that corresponds to a default probability equal to this joint default probability.
This adjusts the default probability of the guaranteed exposure, not its recovery rate. If the exposure guarantee is so strong that the joint probability of default drops to zero, the guaranteed exposure becomes nearly risk-free. It makes sense, in this case, to consider the exposure netted from the guaranteed fraction, which is equivalent to a certain recovery rate equal to this guaranteed exposure. This applies for government guarantees, for instance government owned entities providing guarantees for export-import finance.
A third-party guarantee does not transfer risk to the guarantor to the extent that the joint default probability is much lower than the guarantors default probability. The intuitive notion of risk transfer towards the guarantor overestimates the true risk of primary borrower exposure. Using the guarantor default probability would imply that the joint default probability is equal to that of the guarantor. This cannot be true unless both borrower and guarantor have the same default probability, in addition to perfect correlation. Therefore, this is not an acceptable solution in general unless the guarantor has a zero risk, implying also a zero risk for the exposure.